斜率优化 DP
解决的问题
斜率优化 DP 可以优化以下形式的转移方程:
其中 表示与 有关的函数, 表示与 有关的函数, 代表一个常量。
在上面的式子中,如果 不存在那么就是单调队列或者线段树优化,其余的东西的存在与否并不重要。
解决办法
考虑如果存在 ,满足 且 劣于 (默认取 ,也就是 ,如果是 反过来就行了)。
就有:
化简得到:
发现上面这个东西和 的一次函数很像,那么令 就有:
移项,然后提取公因式:
不妨设 ,注意用的时候不等号的方向,那么同除得到:
总结一下,也就是如果上面的式子成立,那么 比 优秀。
如果令 那么就和求斜率的式子一模一样了,考虑把 搬到直角坐标系里。
下面只考虑不等式是 的情况。
假设三个决策点分别是 , 的斜率是 , 的斜率是 。
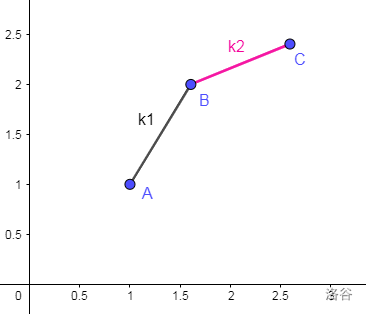
- 如果 ,那么 比 优。
- 如果 ,那么 比 优。
- 显然根据图像有 ,也就是 是一个上凸。
有三种情况:
- ,那么 优于 。
- ,那么 优于 。
- ,那么 优于 。
根据上面的分析,得到结论上凸永远都不可能是最优点。
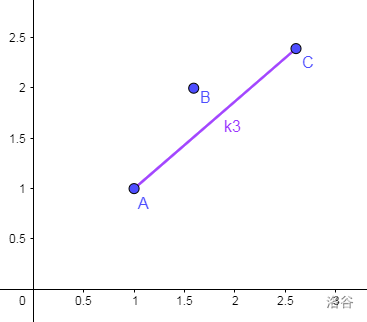
把上凸全部删除之后得到的肯定是一个下凸,也就是这样的东西:

假设下图中的红线是 ,那么肉眼可与看出第 个决策点是最优秀的。
因为 要节点之后的 都大于 ,前面的都小于 。
所以说 就是第 个比 的斜率大的连线的靠前的决策点。
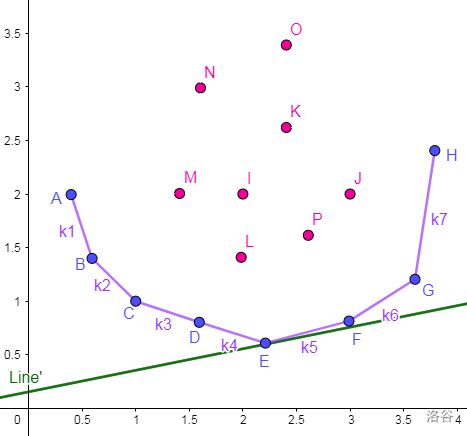
发现因为是下凸,所以有单调性可以二分。
如果有 个决策点,那么这样二分:
double slope(int i,int j){
if(X(j)==X(i)) return Y(j)>=Y(i)?inf:-inf;
return 1.0*(Y(j)-Y(i))/(X(j)-X(i));
}
int F(int k0){
int l=1,r=top-1,p=inf;
while(l<=r){
int mid=(l+r)/2;
if(slope(mid,mid+1)<k0) l=mid+1,p=mid;
else r=mid-1;
}
if(p==inf) return s[1];
return s[p+1];
}
总结
如果是(取 且 单调递增)或者(取 且 单调递减)那么维护下凸。
否则,维护上凸。
注意事项
- 尽量避免使用除法,避免精度误差。
- 注意一些情况需要向凸包内加入如 这样的初始值。
- 注意可能 的值一样,需要加一个 来扰动以下。
- 在把式子整理的时候 其实就是和 无关的东西,不一定要分开。
- 注意是否要保留这样的斜率一样的情况:
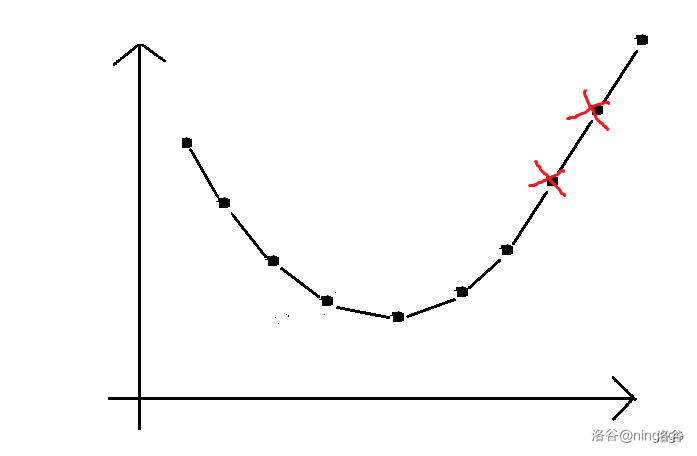
补充
对于 不单调的情况,我们就不能进行直接移项,考虑进行一些奇技淫巧进行调整。
我们考虑分治,先处理左区间,然后再用左区间得到的结果处理右区间。
具体的,把左右区间分别递归完之后再归并排序即可。
整体来说就是一个 CDQ 分治,另外也可以使用李超线段树。
例题
HNOI2008 玩具装箱
令 ,那么有转移方程:
那么把 提前 然后把平方的式子展开,得到:
发现就是上面的形式,且随着 的增长 是不断增长且求解最小值,所以维护下凸。
我们直接二分,然后就做完了。
#include<iostream>
#define int long long
using namespace std;
const int N=5e4+5,inf=1e18;
int n,L,a[N],f[N],s[N],top;
int X(int x){x=s[x];return 2*a[x];}
int Y(int x){x=s[x];return 2*a[x]*L+a[x]*a[x]+f[x];}
double slope(int i,int j){
if(X(j)==X(i)) return Y(j)>=Y(i)?inf:-inf;
return 1.0*(Y(j)-Y(i))/(X(j)-X(i));
}
int F(int k0){
int l=1,r=top-1,p=inf;
while(l<=r){
int mid=(l+r)/2;
if(slope(mid,mid+1)<k0){
l=mid+1,p=mid;
}
else{
r=mid-1;
}
}
if(p==inf) return s[1];
return s[p+1];
}
signed main(){
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin>>n>>L,L++;
for(int i=1;i<=n;i++){
cin>>a[i],a[i]+=a[i-1]+1;
}
s[++top]=0;
for(int i=1;i<=n;i++){
int j=F(a[i]);
f[i]=f[j]+(a[i]-a[j]-L)*(a[i]-a[j]-L),s[0]=i;
while(top>1&&slope(top-1,top)>=slope(top,0)) top--;
s[++top]=i;
}
cout<<f[n]<<'\n';
return 0;
}
CEOI2017 Building Bridges
设 ,考虑前 个柱子并且保留第 个柱子的最小代价。
那么有容易想到朴素的转移方程:
考虑把这个玩意展开,得到:
发现出现了乘积项,考虑使用斜率优化。
注意,因为 有负数所以 不再递增了。
考虑如果 递增,那么下面的分析会假设 以得到 来移项,但是实际上我们并没有直接的使用 和 之间的大小关系。
所以我们可以换一种假设方式,假设 且 比 优。
套路的可以得到不等式:
移项得到:
因为有 ,所以如果按照 排序之后满足下式就可以得到 比 优:
容易发现应该维护下凸壳,考虑让强行让 单调,CDQ 分治即可。
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e5+5,inf=0x3f3f3f3f3f3f3f3f;
int n,h[N],p[N],q[N],s[N],f[N];
int X(int i){return h[i];}
int Y(int i){return f[i]+h[i]*h[i]-s[i];}
int K0(int i){return h[i]+h[i];}
bool cmp1(int a,int b){return h[a]==h[b]?Y(a)>Y(b):h[a]<h[b];}
bool cmp2(int a,int b){return K0(a)<K0(b);}
void solve(int l,int r){
if(l==r) return;
int mid=(l+r)>>1;
solve(l,mid);
sort(p+l,p+1+mid,cmp1);
sort(p+mid+1,p+1+r,cmp2);
int st=1,ed=0;
for(int i=l;i<=mid;i++){
while(st<ed&&(Y(p[i])-Y(q[ed]))*(X(q[ed])-X(q[ed-1]))<=(Y(q[ed])-Y(q[ed-1]))*(X(p[i])-X(q[ed]))) --ed;
q[++ed]=p[i];
}
for(int i=mid+1;i<=r;i++){
while(st<ed&&Y(q[st+1])-Y(q[st])<=K0(p[i])*(X(q[st+1])-X(q[st]))) ++st;
f[p[i]]=min(f[p[i]],f[q[st]]+(h[p[i]]-h[q[st]])*(h[p[i]]-h[q[st]])+(s[p[i]-1]-s[q[st]]));
}
sort(p+l,p+1+r),solve(mid+1,r);
}
signed main(){
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin>>n;
for(int i=1;i<=n;i++) cin>>h[i],p[i]=i;
for(int i=1;i<=n;i++) cin>>s[i],s[i]+=s[i-1];
for(int i=2;i<=n;i++) f[i]=inf;
solve(1,n),cout<<f[n]<<'\n';
return 0;
}
