乱搞 | 一个 OIer 的个人修养

乱搞

· 2025-08-13 · # 笔记

注意到把最后面两行确定了之后会有奇异的效果。

对于图中绿色的点，每一个点可以限制一个黄色的边和一个红色的边，于是我们就建立了一个 $2n-1$ 个限制和 $2n$ 个元素的方程。

那么我们只需要枚举任意一个元素，剩下的操作的都可以递推得到。

于是做完了，时间复杂度为 $O(n^2)$ 。

有个题解有点小问题，其实 $P,Q$ 并不是拓扑序，而是点在拓扑序中的位置。

转化题目的要求，在 $P$ 的逆排列中 $P_{l_i},P_{r_i}$ 出现的先后顺序与 $Q$ 的逆排列中 $Q_{l_i},Q_{r_i}$ 出现的相对位置一定是一样的。

如果我们把 $l_i,r_i$ 连边，然后给这个无向图定向为一个 DAG 那么这个要求就与拓扑序很类似了。

如果 $l_i\to r_i$ ，那么 $l_i$ 这个点一定在拓扑序中出现的位置早于 $r_i$ ，反之同理。

于是现在题目就转化为了，给定一个有向图，将其的边定向构成一个 DAG，要求 $P$ 和 $Q$ 两个该图的拓扑序一样的元素尽可能少。

有一个显然的性质，如果在一个 DAG 上存在一个点 $x$ 满足对于任意的 $y$ 都可以到达 $x$ 或者由 $x$ 到达，那么 $x$ 在拓扑序中的位置就是确定的。

意识流的， $x$ 在图里应该大概长这样：

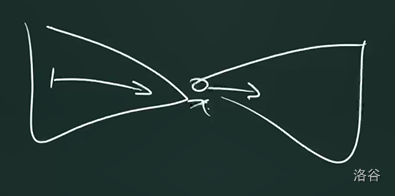
进一步的，其他的位置的点都至少有两个可行的选择，所以我们只需要尽可能的减少在 DAG 中这样的点即可。

又有另外一个很不显然的结论，只有在原图中 $deg=n-1$ 的节点才会成为上述 $x$ 。

如果一个点的 $deg=n-1$ ，那么显然不论 DAG 怎么连边都会让它满足任意的 $y$ 都可以到达它或者由它到达，这是答案的一个下界。

现在，我们只需要构造出一种方案让答案卡到这个下界就可以证明这种方案的最优性。

因为 $deg=n-1$ 的点一定会造成贡献，我们不妨直接把 $deg=n-1$ 的点删除掉。

不妨设在删除结束之后，仍有 $N$ 个点存在，那么取补图，就一定有性质 $\forall x$ 满足 $deg_x>1$ 。

比较简单的情况，如果补图是一个以 $rt$ 为根的菊花图。那么对应到原图上，就是 $rt$ 本身是一个孤立的点，而其他点之间都存在连边。

那么我们可以构造这样的两个拓扑序：

\begin{aligned} rt\to 1\to 2\to \cdots\to n\\ 1\to 2\to \cdots\to n\to rt \end{aligned}

这样的两个拓扑序是没有重复的，于是我们就得到了一种菊花的构造方法。

假设我们遇到的补图不是一个树，那么我们可以直接暴力的删除一些边让它变成一棵树，这种操作对应带原体面上是很好理解，因为多添加一些限制并不会让原本的限制不满足，所以我们可以直接在原图中跑一棵生成树。

现在我们得到了一些树，还是不会做，于是继续加限制也就是删边最终让图组成若干个菊花图就行了。

我们只需要避免出现单独一个点的情况，考虑通过构造的方式证明。

我们给生成树随便找一个点作为根节点，假设其为菊花图的中心，接下来向下 bfs 进行分割。

如果遇到一个点的父亲是中心，直接把他加入父亲中。

如果遇到非叶子节点，那么将其设置为中心，否则如果父亲的菊花大小大于 $3$ 把父亲与合并，否则把父亲设置为中心。

对于具体实现，我们开一个 set 维护一下还没有加入的点就行了。

时间复杂度为 $O((n+m)\log n)$ 。