Arpa’s overnight party and Mehrdad’s silent entering

题目大意

给 $n$ 对情侣染色，要求情侣不能然相同颜色而且相邻 $3$ 人的颜色不同，求合法方案。

数据范围满足 $1\le n\le 10^5$。

思路

钦定 $2i-1$ 与 $2i$ 的人吃的食物不一样，那么这样建图跑出来的一定是二分图。

因为所有图中的换都是由 $x$ 条 $2i-1$ 与 $2i$ 的边与 $x$ 条情侣之间的边组成的长度为 $2x$ 的偶环，一定不存在奇环。

Submission #269643071 - Codeforces

Fortune Wheel - Problem

题目大意

有一个上有编号 $0$ 到 $n-1$ 的转盘，你可以使转盘随机旋转到一个位置或者向前旋转 $k_i$ 个位置，求在最优策略下的期望步数。

数据范围满足，$1\le n\le 10^5,\lvert k \rvert \le 500$。

思路

考虑先使用 bfs，在 $O(n\lvert k\rvert)$ 的时间里求出从任一点通过确定步数移动到 $0$ 的最小步数。

最有策略应该是一直进行随机操作直到到达某一个临界值再使用确定步数的操作完成，所以我们可以枚举每一个临界值选取期望步数最小的一个。

假设这个临界值以内的数构成集合 $S$，那么其移动步数的期望值为 $\dfrac{(\sum\limits_{i\in S}dis_i )+n}{\lvert S\rvert}$ ，可以理解为每一次有 $\dfrac{\lvert S\rvert}{n}$ 的概率随机跳到 $S$ 以内，所以期望次数为 $\dfrac{n}{\lvert S\rvert}$。

Cycle Palindrome

题目大意

给定一个长度为 $n$ 的数列 $a$，要求求出一个排列 $p$ 满足 $a_{p_1},a_{p_2},\cdots ,a_{p_n}$ 是一个回文字符串而且把 $i$ 向 $p_i$ 连边得到的图中只有一个环。

数据范围满足，$1\le \sum n\le 2\times10^5$。

思路

先不考虑 $p$ 是否构成满足要求的环，这样这个题目就很简单了。在构造出了满足 $a_{p_1},a_{p_2},\cdots ,a_{p_n}$ 是回文串的 $p$ 数组之后，考虑哪些 $p$ 中的位置是可以交换的。

1. 如果 $a_{p_i}=a_{p_j}$，那么 $p_i$ 与 $p_j$ 是可以交换的。
2. 可以同时交换 $p_i,p_j$ 和 $p_{n-i+1},p_{n-j+1}$，这样原串的回文性质依旧满足。

在连出的图中，考虑怎么将多个环通过合法的交换合并。

对于下面的这种情况，我们可以在 $a_{p_i}=a_{p_j}$ 的情况下交换 $p_i,p_j$ 将两个环合并。

交换 $p_i,p_j$ 得到：

可以看到这样这两个环就合并了。

但是仅仅合并 $a_{p_i}=a_{p_j}$ 的情况不可以合并所有的环，所以考虑将 $p_i,p_j$ 和 $p_{n-i+1},p_{n-j+1}$ 同时交换。

对于下图这种情况：

先交换 $p_i,p_j$ 和 $p_{n-i+1},p_{n-j+1}$，得到：

再交换 $p_i$ 和 $p_{n-i+1}$，因为 $a$ 序列已经是一个回文串了，所以 $a_{p_i}$ 与 $a_{p_j}$ 注定是一样的。

因为通过第一种合并，我们将所有的 $a_{p_i}$ 的值一样的点全部都到了一个环里，所以在第二个操作中注定可以将能合并的全部合并。

对于具体的实现，考虑使用并查集维护一下是否在一个环中，接着模拟即可。

Submission #269689544 - Codeforces

Playing Around the Table

题目大意

有 $n$ 种牌，一种 $n$ 张，一共 $n$ 个玩家，一人 $n$ 个。每个人一次将一张牌对给下家，求构造方案使可以在 $n\cdot (n-1)$ 次操作之内使第 $i$ 个人拥有 $n$ 张 $i$。

数据范围满足，$1\le n\le 100$。

思路

因为直接构造出题目要求的情况会出现如果一个人提前完成了牌的收集，那么在接下来的操作中他的牌会被打乱，并不足够优秀。

考虑先构造出每一个人都拥有 $1$ 到 $n$ 号牌的方案，在使用 $\dfrac{n\cdot(n-1)}{2}$ 的交换次数交换为题目要求的方案。

现在问题转化为了怎么构造出每一个人都拥有 $1$ 到 $n$ 号牌的方案。

如果没有构造出上述的情况，那么一定有一个人拥有重复的牌，将这个牌传给下家。如果这个人手中的牌都没有重复，那么可以它可以将上家传给他的牌传给下家，这样就可以保证手中现在的情况不被破坏。

只考虑值为 $1$ 的牌需要被往前送多少次。把牌看作 $1$ ，人看作 $−1$ ，那么必然存在一个循环移位使得前缀和非负。于是不难发现，在这个循环移位下，每张牌只会往前走，不会从第 $n$ 个人回到第 $1$ 个人。

所以这个操作是可以在 $\dfrac{n\cdot(n-1)}{2}$ 次操作之内完成的。

Submission #269726457 - Codeforces

Winter 2021 Day4I Color

题目大意

给定一个 $n$ 个点的完全图，每条边都被染了 $m$ 种颜色中的一种。

你需要判断能否再加入 $m − n + 1$ 个点，补成一个 $m + 1$ 个点的完全图，并且每条边仍然被染了 $m$ 种颜色中的一种，使得每个点都满足相邻的边的颜色恰好取遍这 $m$ 种。

思路

先把原图不合法和 $m$ 是偶数的情况判断掉。

在最终的图中会有一条边会有 $3$ 种情况：

• 对于两个端点都已经确定的情况，我们把这样的边加入这个颜色的 2-set。
• 对于有一个端点确定的情况，我们把这样的边加入这个颜色的 1-set。
• 对于有没有端点确定的情况，我们把这样的边加入这个颜色的 0-set。

如果一个颜色的 1-set 和 2-set 的大小加起来比 $\dfrac{m+1}{2}$ 还要大，那么显然是无解的。

否则，我们可以考虑证明其一定是有界的，具体的只需要证明可以新加入一个点然后是合法的就行了。

那么容易想到用二分图跑最大流来进行这个拓展：

左边放 $m$ 个点表示 $m$ 种颜色，右边放 $n+1$ 个点，前 $n$ 个点表示和新加入的点的连边颜色，而最后面的点是还没有考虑的点与新加的点匹配。

如果第 $x$ 个点周围没有颜色 $i$，那么就把颜色 $i$ 与 $x$ 点连接为流量为 $1$ 的边。

如果 $x,i$ 匹配那么就代表新加入的点要与 $x$ 连接一个颜色为 $i$ 的边。

另外每个颜色还要和右边的第 $n+1$ 个点连接一条流量为 $1$ 的边，代表新加的这个点的这个颜色以后再匹配。

特殊的，第 $n+1$ 个点向汇点的流量是 $m-n$，根据其定义容易理解。

在跑了网络流之后去更新 $3$ 个 set 的数据就行了。

显然如果我们跑了满流，那么就代表我们成功的拓展了一次，但是似乎很难证明这个东西一定是满流。

我们引入了一个牛逼定理（pb 都不会证的那种），就是每个点的都都一样的二分图一定可以跑满流。

那么因为每一个节点的流量最大都只有 $1$，那么如果我们可以在中间随便多连一些边或者把一些点拆爆然后乱搞去凑上面的定理。

pb 使用的方法是让所有的颜色都给右边 $n+1$ 连 $2$ 倍 0-set 的点，这样出去右边 $n+1$ 所有的点都是 $m-n+1$ 个出边。

发现左边的节点是 $m-n+1$ 有点不好证，考虑对于一种颜色，把其边的对应的端点用表格的方式表现出来，不知道的留空。

那么 $1-set$ 有 $1$ 个空子，$2-set$ 没有空子，$0-set$ 有两个空子，所以空子的数量就是 $2\times S_0+S1$。

用另一种角度考虑，其实这个空子的数量也是 $m-n+1$ 因为格子里面一共加入了 $n$ 个点而一共有 $m+1$ 个点，于是得证。

这个时候右边 $n+1$ 的点连了 $(m-n)\times (m-n+1)$ 条边，那么我们直接把这个点拆爆成 $m-n$ 个，这样我们就凑出了牛逼定理，也就证明了做法的正确性。

1st ucup stage 3 F Flower Garden

题目大意

构造长度为 $3n$ 的 $01$ 字符串，要求至少有 $n$ 个 $0$ 和至少 $n$ 个 $1$。

给定 $a_i,b_i,c_i,d_i$，要求 $[a_i,b_i]$ 全部都是 $0$ 或者 $[c_i,d_i]$ 全部都是 $1$，构造任意合法解或者报告无解。

思路

如果没有至少为 $n$ 的要求，那么我们可以用 $x\to y$ 表示如果 $s_x=1$ 那么 $s_y=1$。

线段树优化建图，然后跑 tarjan 缩点，一个强连通分量里的点都是有确定关系的。

考虑回原问题，给定一个有点权的 DAG，把它切成两半要求任何一半的权值都在 $[n,2n]$ 之间。

如果有一个点的权值大于 $n$，那么把这个点和前驱放一起或者和后驱放一起，枚举一下就行了。

否则拓扑序一个一个加，想停就停一定可以找到一个合法的情况。

CF1844E Great Grids

容易发现，确定了 $(x-1,y-1),(x-1,y),(x,y-1)$ 之后 $(x,y)$ 就是一定的了。

于是假设处理了边边然后打表发现有一些奇异的规律：

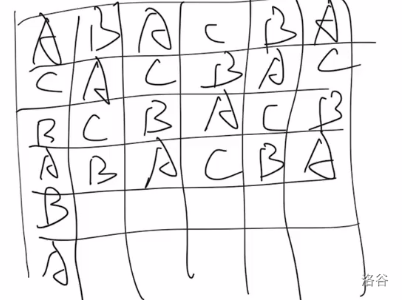
上图为 pb 大佬亲笔书写。

注意到如果把 $A,B,C$ 看成 $0,1,2$ 那么行与行之间就是在模 $3$ 意义下增加了一个常数，列与列之间也是同理。

我们不妨设 $(1,1)$ 这个位置为 $0$，第 $i$ 行与第 $1$ 行相差 $a_i$，第 $j$ 列与第 $1$ 列相差 $b_i$。

所以我们只需要确定 $a,b$ 数组，那么整个方阵就确定了。

对于题目给出的限制无非就是类似于 $a_i-a_{i-1}=b_{j}-b_{j+1}$ 或者 $a_i-a_{i-1}=b_{j}-b_{j-1}$。

因为都是连续的，那么我们不妨维护 $A_i=a_{i}-a_{i-1}$ 和 $B_{i}=b_i-b_{i-1}$，最后用并查集 xjb 维护一下就行了。

Empty up a Bottle

容易发现，进行一次操作相当于：

$\begin{aligned} A\gets 2A\bmod (A+B)\\ B\gets 2B\bmod (A+B) \end{aligned}$

如果 $A+B$ 为奇数，就有：

$2^{\varphi(A+B)}\equiv 1\pmod{A+B}$

于是我们就有了除法，所以就很牛逼。

我们不妨假设 $A,B$ 为偶数，$C$ 为奇数，对于其他的情况我们都可以将其转化为这种情况。

假设都是奇数，那么随便找两个处理一下就是我们需要的情况。

假设都是偶数，那么我们假设他们全部除以 $2$，不进行操作，因为全部乘以倍数并不影响我们后面的构造。

在得到希望的情况之后，不妨假设 $B>A$，我们有构造：

$\{A,B,C\}\to \{2A,B-A,C\}\to\{A,B-A,C+A\}$

如果没有次数限制，那么我们反复进行上述操作，用类似于辗转相减法一定可以最后得到 $0$。

但是如果 $B$ 远大于 $A$，$500$ 次肯定不够用，于是我们考虑在让 $B$ 减去 $2^k$，加速处理。

那么我们有更新的构造：

$\begin{aligned} &\{A,B,C\}\\ &\{2^kA\bmod (A+C),B,2^{k}C\bmod (A+C)\}\\ &\{2^{k+1}A\bmod (A+C),B-2^{k}A,2^kC\bmod (A+C)\}\\ &\{2^{k}A,B-2^kA,C-2^{k+1}A\bmod (A+C)\}\\ &\{A,B-2^kA,\dfrac{C}{2^k}-2\bmod (A+C)\} \end{aligned}$

显然 $C$ 的值会一直保持为奇数，因为 $3$ 个数的和是一定的，$A,B$ 始终为偶数。

于是通过这个神奇的构造，模拟即可。