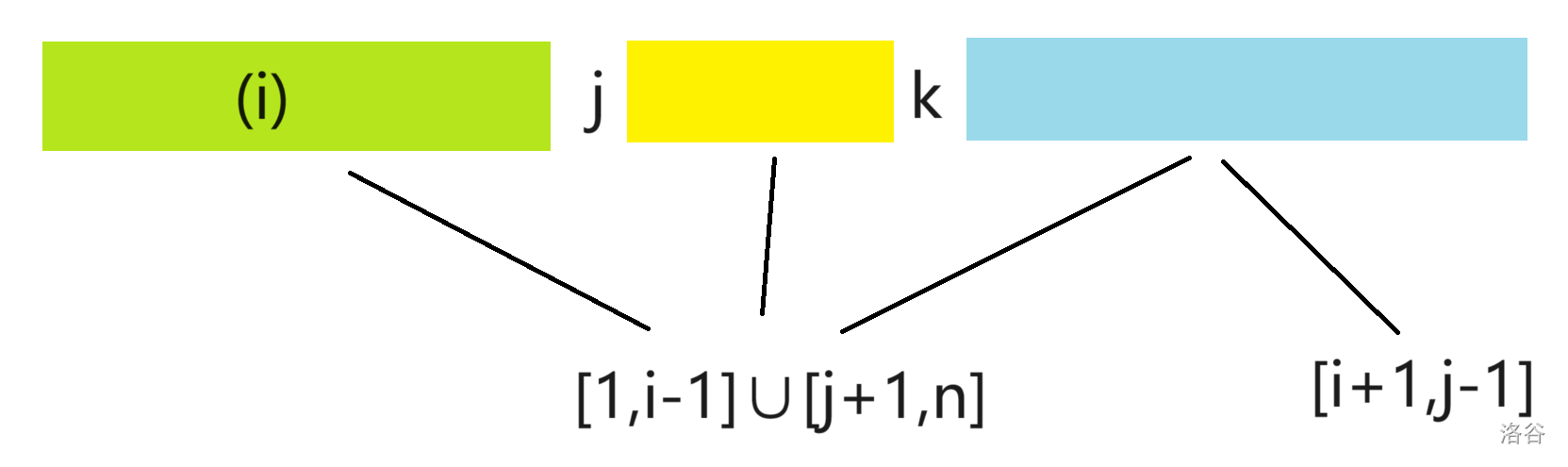雅礼集训 2017 Day5珠宝

把价格一样的分到一起，然后按照价值进行排序。

那么设 $f_{i,j}$ 表示前 $i$ 组的物品使用了 $j$ 的空间的最优情况，那么有转移方程：

$f_{i,j}=\max\{f_{i-1,j-k\times i}+w_{i,k},f_{i-1,j}\}$

有一种很牛逼的想法，因为所有的 $j-i\times k$ 再对 $i$ 取模的意义下是一样的，所以我们可以把在模 $i$ 意义下一样的按照 $i$ 的几倍为下表塞到另一个数组里 DP。

很难想到这个东西是有决策单调性的，因为如果 $j-k\times i$ 比 $j-p\times i$ 优而且 $p>k$ 那么，那么比 $p$ 大的决策点都是更裂的。

于是进行分治处理就行了，时间复杂度为 $O(mc\log n)$。

四边形不等式优化

ARC201B Binary Knapsack

其实可以不用上面的方法，直接把代价从小到大处理，如果 $W$ 这一位是 $1$ 那么买一个。

把两个两个的放到上一组去，继续跑就行了。

NOIP2021 数列

去维护那些位置最后是 $1$ 显然不现实，我们可以考虑之记录现在的最高位 $p$，让以后之后 $p$ 会去进位。

那么我们考虑设 $f_{i,j,k,p}$ 表示考虑了 $S$ 的后第 $i$ 位（最低位为 $0$）之后，在 $a$ 中确定了 $j$ 个位置，$S$ 里面有 $k$ 个 $1$，以前的操作向现在贡献了 $p$ 个进位。

那么有方程：

$f_{i+1,j+t,k+(t+p)\bmod 2,\lfloor\frac{t+p}{2}\rfloor}\gets f_{i+1,j+t,k+(t+p)\bmod 2,\lfloor\frac{t+p}{2}\rfloor}+f_{i,j,k,p}\times {v_i}^t\times {n-j\choose t}$

最后加上 $\operatorname{popcount}$ 判断一下合法就行了，时间复杂度为 $O(n^4m)$。

ARC200E popcount<=2

其实有点难，但是容易想到的是令 $a_1=0$ 最后再乘上 $2^m$。

这个题目的难点在于，如果把一堆情况以西讨论很容易算重或者算漏，明智的做法应该是分成若干种中互斥的子情况进行逐一计数。

最容易想到的是 $\operatorname{popcount}\le 1$ 的情况：

$(m+1)^{n-1}$

然后是再不考虑 $0$ 的情况下，只有一个数 $\operatorname{popcount}=2$ 的情况：

${m\choose 2}(4^{n-1}-3^{n-1})$

那么它所有的子集都是合法的，所以有 $4$ 中情况，再减去没有他自己的情况。

接下来是有三个 $\operatorname{popcount}=2$ 的数而且他们的 $\&= 0$，形如 $0,3,0,5,5,6,0,3$：

${m\choose 3}(4^{n-1}-3\times 3^{n-1}+3\times 2^{n-1}-1)$

考虑一种所有的 $\operatorname{popcount}=2$ 的数某一位都是 $1$：

$m\times((m+1)^{n-1}-2^{n-1})$

但是发现最后两种情况其实有重复的，即只有一个 $\operatorname{popcount}=1$ 和 $\operatorname{popcount}=2$ 的数，而且满足之间的包含关系，把这种情况干掉就行了。

$m\times(m-1)\times (3^{n-1}-2^{n-1})$

于是答案就是：

$2^{m}\times \{(m+1)^{n-1}+{m\choose 2}(4^{n-1}-3^{n-1})+{m\choose 3}(4^{n-1}-3\times 3^{n-1}+2\times 2^{n-1}-1)+m\times((m+1)^{n-1}-2^{n-1})-m\times(m-1)\times (3^{n-1}-2^{n-1})\}$

做就完了。

CF2108F Fallen Towers

一个比较有意思的题目，考虑一个性质：

对于一个已经操作完的序列，我们可以通过一些操作的顺序改变，达到在不改变其他位置的情况下，让某一特定位置减少 $1$ 的效果。

考虑怎么通过构造的手段达到这个效果，对于第 $x$ 个位置，我们可以让其被推到的时候向后延一次，那么自然就达到了效果。

问题是这个操作会让后面的某一个位置多一个，那么我们不妨对后面的位置再进行一次操作，最后我们就可以把它转移到 $n$ 之外忽略掉，于是我们就得到了方法。

那么容易理解这个东西是有单调性的，因为如果较高的都可以做出来，那么直接给它们全部减 $1$ 就可以了。

也容易理解最后得到的序列是 $0,0,\cdots,0,1,2,\cdots,k-1,k$ 的形式的。

于是二分判断，考虑怎么贪心的搞，设二分出来的答案是 $x+1$，那么第 $i$ 个位置的权值就为 $r_i=\max(0,x+i-n)$，于是我们从前向后推到。

假设现在前面对这个位置的贡献为 $now$，那么如果 $now<r_i$ 则定然无解。

那么我们考虑给他留下 $r_i$ 向后面的 $[i+1,i+a_i+now-r_i]$ 每个位置贡献 $1$。

那么开个什么东西随便维护一下就行了，时间复杂度为 $O(n\log n)$。

ABC219H Candles

以前做了没写，现在补一下。

套路的，我们记 $f_{l,r,k,0/1}$ 表示选择了区间 $[l,r]$ 有 $k$ 根蜡烛还在燃烧，现在在 $l$ 或者 $r$。

因为我们每移动一个位置仍然燃烧的 $k$ 根蜡烛就会降低 $1$，于是考虑把费用提前计算。

遇到一个蜡烛，我们分别考虑熄灭和不熄灭。

因为题目要求的情况 $k$ 肯定势在刚好取到正确值且不拿负数蜡烛的时候，所以我们直接 DP 就行了。

USACO19JAN Redistricting P

令 $f_i$ 表示前 $i$ 的答案，$s_i$ 为 $H,G$ 的前缀和（$H$ 为 $1$），那么有：

$f_{i}=\min\limits_{j=\max(1,i-k)}^{i-1} f_j+[s_i-s_{j-1}\ge 0]$

那么我们把 $f$ 按照 $s$ 进行排序添加到一个线段树里面，这样就是区间加 $1$，然后单点改和全局查，做完了。

ZhenDeHaoNanXieA！

USACO20JAN Springboards G

肯定是从一些跳板跳到另一些跳板，那么我们不妨设 $f_i$ 表示在 $i$ 跳板结束的最少步数。

那么我们按照从左下角到右上角把跳板排一个序，然后就有方程：

$f_i=\min\limits_{i=0}^{i-1} f_j+(x_i-x_j')+(y_i-y_j')$

把里面打开：

$f_i=x_i+y_i+\min\limits_{j=0}^{i-1} f_j-x_{j}'-y_j'$

我们直接把后面的一堆东西随便取一个最小值就行了，时间复杂度为 $O(n\log n)$。

AGC043D Merge Triplets

很难想到 $P$ 一定是一个这样的东西：

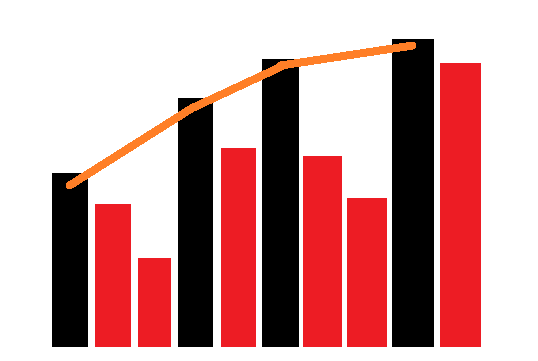
具体的，如果我们把递减的放到一起，那么一组的大小一定介于 $[1,3]$ 而且每一组的开头是逐渐增加的。

感性理解可以得到：

如果满足 $2$ 的个数大于 $1$ 的个数，而且 $1,2,3$ 总共使用的加一起是 $3n$，那么就一定是合法的。

假设我们规定第 $i$ 组的元素个数为 $n_i$，那么在一个定了的组的方案数为：

$\dfrac{n!}{\prod\limits_{i=1}^k(\sum\limits_{j=1}^i n_i)}$

我们可以这样理解，我们随便拿到一个 $a$，然后在 $[1,a_i]$ 中显然最大的应该放在一开始的位置。

有 $a_i$ 种方案但是现在只有 $1$ 种了，于是就除以了 $a_i$，后面的以此类推。

我们考虑用 DP 求出有多少合法的划分方法，于是我们设 $f_{i,j}$ 表示考虑了前 $i$ 个位置的元素，$1$ 个长度减去 $2$ 个长度的数量。

那么有方程式：

$f_{i+1,j+1}\gets f_{i+1,j+1}+f_{i,j}$

其中 $i+1$ 被约掉了。

$f_{i+2,j-1}\gets f_{i+2,j-1}+f_{i,j}\times (i+1)$

其中 $i+2$ 被约调了。

$f_{i+3,j}\gets f_{i+3,j}+f_{i,j}\times (i+1)\times (i+2)$

其中 $i+3$ 被约调了。

最后答案就是：

$\sum\limits_{i=1}^{3n} f_{3n,i}$

CF1854B Earn or Unlock

比较好想，非常难想。

考虑如果一个区间 $[1,k]$ 刚好全部用了，那么获得的收益是 $1+\sum\limits_{i=1}^k (a_i-1)$，之所以减 $1$ 是因为需要一次机会来解锁它。

那么设 $f_i$ 表示 $[1,i]$ 是否可以完全解锁，那么有方程：

$f_j=f_j\text{ or }f_{j-a_i}$

用 bitset 优化一下就行了。

AGC033D Complexity

容易想到一个暴力 DP，设 $f_{i,j,k,l}$ 表示考虑了 $(i,j)$ 到 $(k,l)$ 的区域的最小代价。

那么直接转移是 $O(n^5)$ 的，考虑能不能把状态优化掉。

很难发现其实答案的值域为 $O(\log n+\log m)$，而且取值是单调的。

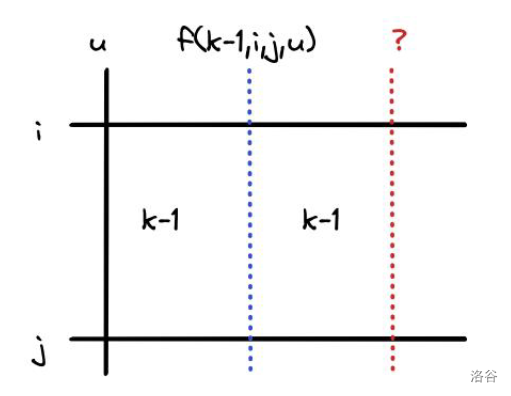
所以套路的，我们设 $f_{l,i,j,k}$ 表示在代价为 $l$ 的情况下，最大可以考虑 $(i,k)$ 到 $(j,f_{l,i,j,k})$。

考虑怎么转移，对于下图的转移方式，容易想到方程式：

$f_{l,i,j,k}=f_{l-1,i,j,f_{l-1,i,j,k}+1}$

对于下图的情况，也同样容易想到方程式：

$f_{l,i,j,k}=\max\limits_{t=i}^{j-1} \min(f_{l-1,i,t,k},f_{l-1,t+1,j,k})$

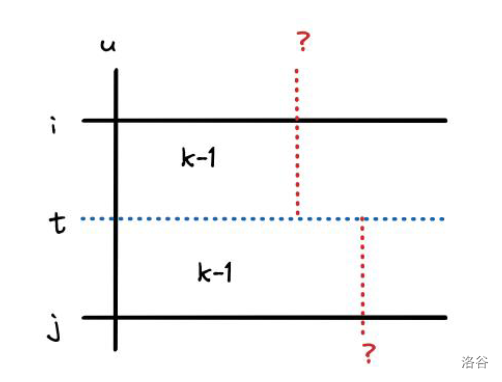
现在的时间复杂度为 $O(n^4\log n)$ 瓶颈在于横着这种转移，考虑优化。

容易发现当 $t$ 增加时 $f_{l-1,i,t,k}$ 是增加的而 $f_{l-1,t+1,j,k}$ 是减少的，于是考虑二分找到最中间的位置，现在时间复杂度为 $O(n^3\log^2n)$。

USACO24DEC Interstellar Intervals G

首先需要做的是正确的理解题目：

• 首先，区间的长度是自己确定的。
• 其次，这是一个计数题。

有一个很帅的性质，$[j,i]$ 可以用一次染色解决与下面的一坨东西是充要条件：

• $len=i-j+1$ 需要是一个偶数。
• 设 $j$ 后面离 $j$ 最近的蓝色是位置 $x_j$，那么 $i-x_j+1\le \dfrac{len}{2}$。
• 设 $i$ 前面离 $i$ 最近的红色是位置 $y_i$，那么 $y_i-j+1\le \dfrac{len}{2}$。

于是接下来的暴力就很好想了，我们设 $f_i$ 表示前 $i$ 个位置考虑了之后的最小代价。

转移方程如下：

$f_i\left\{\begin{matrix} 0& s_i=\texttt{R}\\ f_{i-1}& s_i=\texttt{X} \\ \sum\limits_{in[j,i]}& s_i=\texttt{X},\texttt{B}\\\end{matrix}\right.$

其中 $in[j,i]$ 表示区间 $[j,i]$ 合法，合法的判断可以预处理，时间复杂度为 $O(n^2)$。

考虑优化，对于这样的东西线段树是一个很套路也很好用的选择。

我们考虑给 $f$ 的转移按照奇偶性的不同开两棵树，这样就解决了 $j-i+1$ 是偶数的要求了。

那么把上面性质里的式子进行一下简单的变形，得到：

$i\le 2x_j-j-1,j\ge 2y_i-i+1$

那么把 $2x_j-j-1$ 放到一个优先队列里面，然后在线段树里面访问 $[2y_i-i+1,i)$ 的和就行了。

USACO21DEC HILO P

从有贡献的 $(j,k)$ 为角度进行讨论，其中 $i$ 为 $max[1,j)$：

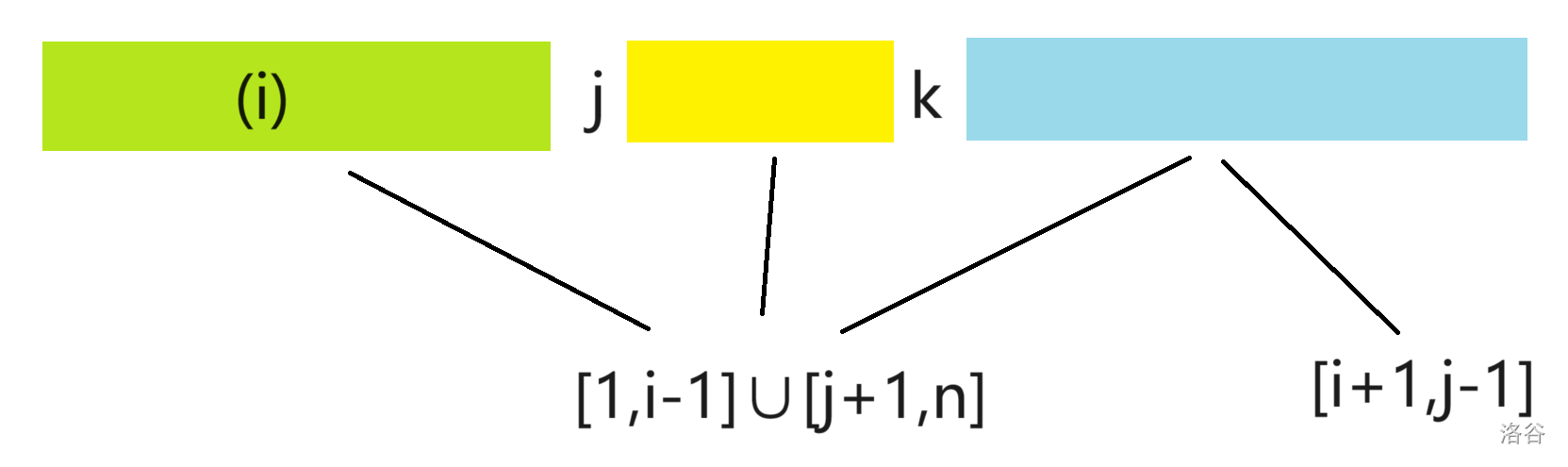
发现其他数防止与 $k$ 没有关系，于是枚举 $i,j$ 得到：

$A_{n-j+\max(i-1,0)}^{n}\times (x-i)\times(j-i-2)!$

其中第 $1$ 项是 $[1,i)\cup(j+1,n]$ 的方案数，$x-i$ 是 $k$ 的方案数，$(j-i-2)!$ 是 $(i,j)/\{k\}$ 的方案数。

打开得到：

$n!\sum\limits_{i=1}^{x-1}(x-i)\sum\limits_{i=x+1}^{n}\dfrac{1}{(j-i+1)\times (j-i)\times (j-i-1)}$

于是时间复杂度为 $O(n^2)$，不想优化了。

CF985E Pencils and Boxes

拍一个序，设 $f_i$ 表示 $[1,i]$ 是否有合法的方案，那么有转移：

$f_i=\text{Or}_{a_i-a_j\le d\wedge i-j+1\ge d}\ f_{j-1}$

那么直接维护一下区间和就行了。

POI 2014 PTA-Little Bird

设 $f_i$ 表示在 $i$ 结束的最小代价，那么有：

$f_{i}=\min\limits_{j-i+1\le k} f_{j}+[a_i\ge a_j]$

不会做，把 $a_i$ 排序之后用线段树随便维护一下就行了。

集训队互测 2012 calc

简单的思维，设 $f_{i,j}$ 表示考虑 $[1,i]$ 使用的数为 $[1,j]$ 单调递增的方案数，最后答案乘 $n!$ 就行了。

那么有转移：

$f_{i,j}=f_{i-1,j-1}\times j+f_{i,j-1}$

有一个天才的想法，有没有可能最后的答案可以用一个多项式表达呢？

注意到 $f$ 的转移不是很容易看出多项式的次数，我们令 $g_{i,j}$ 表示选择的恰好为 $j$ 的方案数，那么有方程：

$g_{i,j}=j\times \sum\limits_{k=0}^{j-1} g_{i-1,k}$

前缀和加一个，乘 $j$ 再加一个，最后次数为 $2n$。

那么有因为：

$f_{n,A}=\sum\limits_{j=0}^A g_{n,j}$

所以 $f_{n}(A)$ 为一个 $2n+1$ 次函数，直接拉格朗日插值就行了。

ICPC 2022 Jinan R Skills

比较拟人的一个题目，考虑暴力 DP。

设 $f_{i,j,k,l}$ 表示现在联系的项目是 $j$，另外两个项目上一次的时间是 $k,l$，状态数是 $O(n^3)$ 的无法通过。

有一个比较厉害的性质，如果一个项目开始练习了，那么距离下一次联系的时间一定是小于等于 $\sqrt{A_{mx}}+O(1)$。

感性理解，如果超过 $\sqrt{A_mx}+O(1)$ 天之后以前的技能点就掉光了，不如不点。

其中 $O(1)$ 应该取 $3$ 比较合适，因为可能还有其它的技能也需要点技能点。

那么我们把状态改为 $f_{i,j,k,l}$ 表示现在联系的项目为 $j$，另外两个项目距离上一次联系已经过了 $k,l$ 天，那么现在的状态数就是 $O(n^2)$ 的了，转移是 $O(1)$ 的做完了。

USTCPC 2025 生成树！

谢谢䟀㭸瑞璶。

考虑枚举两个与 $0$ 相连的点的间隔 $p_1k, p_2k, \cdots, p_tk$。

$p_1k$ 是 $1$ 和最后一个点的距离，显然有 $\sum p_ik = n$，即 $\sum p_i = \frac{n}{k}$。

现在我们考虑第一个点的方案数，为了不与其他方案算重所以第 $1$ 个点只有 $p_1$ 中选择，而在两个被选择的点之间必须要断开一条边。

那么我们现在就可以书写答案的代数表达式 ${\sum\limits_{\sum p_i = \frac{n}{k}} p_1 \prod p_ik}$ 。

设 $f(n) = \sum\limits_{\sum p_i = n} p_1 \prod p_ik$。

我们考虑构造 $f(n)$ 的递推式：

$\begin{array}{} f(n - 1) = \sum\limits_{\sum p_i = n - 1} p_1 \prod p_ik \\ f(n - j) = \sum\limits_{\sum p_i = n - j} p_1 (\prod p_ik) \end{array}$

我们观察它们和 $f(n)$ 的区别就是和少了 $j$，那么我们可以添加新的 $p_{t + 1} = j$，但是这样就少算了 $t = 1$ 的情况，因此我们在加上 $t = 1$ 且 $p_t = n$ 的答案。

此时我们就得到了 $f(n)$ 的递推式：

$f(n) = n ^ 2 k + k \sum\limits_{j = 1} ^ {n - 1} (n - j) f(j)$

现在我们将其化简：

$f(n) - f(n - 1) = (2n - 1)k + k \sum\limits_{j = 1} ^ {n - 1} f(j)$

因此：

$f(n) = f(n - 1) + (2n - 1) k + k\sum\limits_{j = 1} ^ {n - 1} f(j)$

因此我们维护 $a_n = f(n), b_n = \sum\limits_{j = 1} ^ n f(n), c_n = 2n + 1$。

改写为矩阵可以得到：

$\left[ \begin{matrix} a_i & b_i & c_i & 1 \end{matrix} \right] \times \left[ \begin{matrix} 1 & 1 & 0 & 0 \\ k & k + 1 & 0 & 0\\ k & k & 1 & 0\\ 0 & 0 & 2 & 1 \end{matrix} \right] = \left[ \begin{matrix} a_{i + 1} & b_{i + 1} & c_{i + 1} & 1 \end{matrix} \right]$

初始时 $a_1 = k, b_1 = k, c_1 = 3$。

POI 2013 LUK-Triumphal arch

显然向回走的不明智的，考虑我们设 $f_i$ 表示不给 $i$ 染色的情况下 $i$ 这个子树需要多少外来的情况才可以把除 $i$ 以外的点全部染黑。

那么显然有转移：

$f_{i}=\max(\sum\limits_{x\in son_i} (1+f_{j})-k,0)$

时间复杂度为 $O(n)$，做完了。

POI 2014 FAR-Farm Craft

容易想到，这个操作相当于确定每一个叶子的访问顺序。

而题目要求走到一个点就必须把它的子树全处理了，而且最优的情况一定是遇到了就马上安。

所以我们设 $f_{i}$ 表示 $i$ 子树全部安装完的时间花费，$g_i$ 表示 $i$ 子树遍历一遍的时间花费。

那么 $i$ 子树的等待时间就是 $f_i-g_i$，为了让所有等待的时间都尽可能不要影响到答案，我们按照 $f_i-g_i$ 从大到小处理。

于是有换转移：

$g_x\gets\sum\limits_{i\in son_x} g_i+2$

假设把 $son_x$ 中所有的点都按照 $f_i-g_i$ 排序之后，那么：

$f_x\gets \max\{c_x,\max\limits_{i=1}^{\lvert son_x\rvert} f_i+\sum\limits_{j=1}^{i-1} g_j\}$

时间复杂度为 $O(n\log n+m)$。

USACO10MAR Great Cow Gathering G

换根 DP 板子题。

我们设 $f_i$ 表示在 $1$ 为根的情况下 $i$ 的子树转移到 $1$ 的最小代价，那么有方程：

$f_x\gets\sum\limits_{i\in son_x} (f_i+siz_i\times w_{x,i})$

考虑换根，原来 $x$ 是根，现在换成 $y$。

$f_x=\sum_{i\in Other} f_i+f_y+siz_y\times w_{x,y}$

那么我们进行下面的操作：

$f_x\gets f_x-f_y-siz_y\times w_{x,y}$

$f_y\gets f_y+f_x+(n-siz_y)\times w_{x,y}$

NOIP2022 建造军营

题目大意

给一张 $n$ 个点 $m$ 条边的无向图，选择一些点和一些边，使得删掉任意一条没有选择的边不会使得两个选择的点不连通，求方案数。

思路

比较奇妙的题目。

容易理解对于一个边双，显然不论删掉哪个都不会导致不联通。

那么我们把点双全部都拿出来缩成一个点，那么原图就变成了一棵树。

我们设 $f_{x,0/1}$ 表示在以 $x$ 为根的子树中，是否选择军营的方案数。

• $i$ 子树里面没有军营，目前 $x$ 里也没有军营，那么这个边可以乱选：

$f_{x,0}\gets f_{x,0}\times f_{i,0}\times 2$

• $i$ 子树里面没有军营，目前 $x$ 里面有军营，那么这个边也可以乱选：

$f_{x,1}\gets f_{x,1}\times f_{i,0}\times 2$

• $i$ 子树里有军营，目前 $x$ 里面没有军营，那么这个边必须选：

$f_{x,1}\gets f_{x,0}\times f_{i,1}$

• $i$ 子树里有军营，目前 $x$ 里面也有军营，那么这个边必须选：

$f_{x,1}\gets f_{x,1}\times f_{i,1}$

上面的东西是同时进行了，那么整理一下得到：

$f_{x,0}\gets 2\times f_{x,0}\times f_{i,0}$

$f_{x,1}\gets f_{x,1}\times (f_{i,1}+2\times f_{i,0})+f_{x,0}\times f_{i,1}$

对于初始化，我们令一个边双的节点数量为 $s_x$，那么：

$f_{x,0}=1,f_{x,1}=2^{s_x}-1$

对于答案，我们记子树的大小为 $siz$，那么答案为：

$\sum\limits_{x=1}^n f_{x,1}\times 2^{m-siz_x+[i=1]}$

于是做完了。

ARC171C Swap on Tree

考虑有一个性质，对于一个子树，通过题目的操作最多只会有 $1$ 个外来的节点进入，而且不管进入的是什么东西都不影响结果的方案数。

于是我们可以设 $f_{x,i,0/1}$ 表示在以 $x$ 为根的子树中，与 $x$ 相连的边断了 $i$ 条，是否都与父亲的边断掉了，其中 $i$ 包括断掉父亲的边。

枚举其儿子，转移即可：

$\begin{aligned} f'_{u,i,0}&\gets f_{u,i,0}\times g_{v,0}+[i>0]\times f_{u,i-1,0}\times i\times g_{v,1}\\ f'_{u,i,1}&\gets f_{u,i,1}\times g_{v,0}+[i>1]\times f_{u,i-1,1}\times i\times g_{v,1} \end{aligned}$

其中两个转移式的前一项代表不断 $(u,v)$ 这条边，后一项代表断 $(u,v)$ 这条边，乘以 $i$ 是为了确定与 $u$ 相连的 $i$ 条边的断边顺序。

时间复杂度 $O(n^2)$。

ABC222F Expensive Expense

很板的一个题，我们考虑先拟定 $1$ 为根跑一个 DP。

我们设 $f_i$ 表示以 $i$ 为根的子树中的最大值，$g_i$ 表示以 $i$ 为根的子树中的次大值。

转移是容易的，考虑怎么换根。

假设 $i$ 是 $x$ 的儿子且现在拟定以 $x$ 为根，那么相当于让 $x$ 少考虑 $i$，让 $i$ 所考虑 $x$。

那么如果 $f_x=f_i+w(i,x)$，则 $f_x\gets g_x$。

接着我们让 $x$ 去考虑 $i$ 就行了，具体的在跑一次前面的转移即可。

做完了，时间复杂度为 $O(n)$。

JSOI2018 潜入行动

考虑设 $f_{x,i,0/1,0/1}$ 表示考虑了以 $x$ 为根的子树，内部放置了 $i$ 个窃听器，且 $x$ 节点是否安装了窃听器，是否被窃听的方案数。

那么显然有转移：

$f_{x,i+j,0,0}=\sum f_{x,i,0,0}\times f_{p,j,0,1}$

$f_{x,i+j,1,0}=\sum f_{x,i,1,0}\times (f_{p,j,0,0}+f_{p,j,0,1})$

$f_{x,i+j,0,1}=\sum f_{x,i,0,1}\times (f_{p,j,0,1}+f_{p,j,1,1})+f_{x,i,0,0}\times f_{p,j,1,1}$

$f_{x,i+j,1,1}=\sum (f_{x,i,1,0}\times (f_{p,j,1,0}+f_{p,j,1,1})+f_{x,i,1,1}\times (f_{p,j,0,0}+f_{p,j,0,1}+f_{p,j,1,0}+f_{p,j,1,1}))$

USACO25FEB Bessie's Function G

很帅的一个题。

容易发现 $i\to a_i$ 之后一定形成一个内向基环树，那么有一个思路。

我们可以把基环树理解成这样：

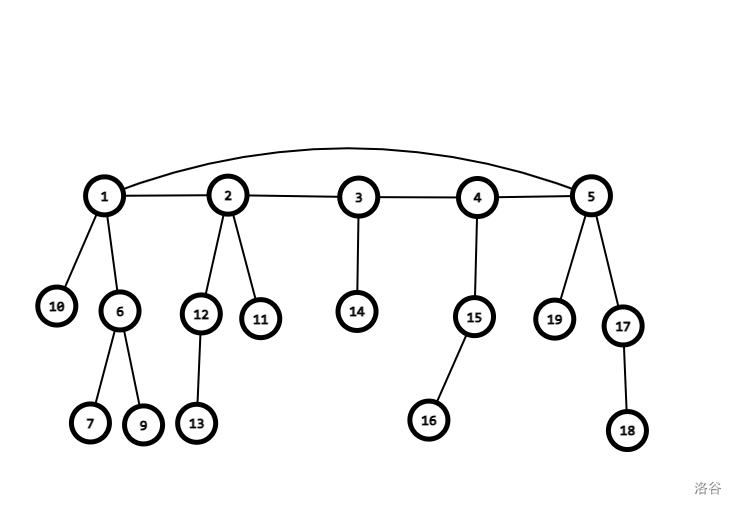
那么就容易理解，我们把环和树分开处理。

有一个显然的性质，如果要求改 $a_i$，那么一定是 $a_i\gets i$。

题目的要求就是一堆自环，然后其他的点向它连边都成一个类似于菊花的东西。

那么直接设 $f_{i,0/1}$ 表示第 $i$ 个点是否是自环的最小值。

那么：

$f_{i,0}=\sum f_{p,1}$

$f_{i,1}=\sum\min(f_{p,0},f_{p,1})$

那么环转移方程：

$g_{i,0,0/1}=f_{ring_i,0}+\min(g_{i-1,0,0/1},g_{i-1,1,0/1})$

$g_{i,1,0/1}=f_{ring_i,1}+g_{i-1,0,0/1}$

其中最后一维表示起点的选择情况，转移即可。

于是做完了，时间复杂度为 $O(n)$。

AGC061C First Come First Serve

比较容易漏掉的是 $\forall i<n,a_i<a_{i+1},b_{i}<b_{i+1}$。

考虑当 $(a_i,b_i)$ 会对答案造成 $2$ 次当且仅当 $(a_i,b_i)$ 中有被选择的点，那么我们就可以设 $f_i$ 表示考虑了 $1$ 到 $i$ 的方案数。

于是考虑容斥，显然 $f_i\gets 2\times f_{i-1}$。

需要注意的，不可能有包含关系。

那么如果我们找到最大的 $b_j<a_i$ 且 $a_k<b_i$，则 $(j,k]$ 区间只有在至少一个在 $(a_i,b_i)$ 中选择才会有效果，于是我们 $f_k\gets f_{k}-f_{j}$，相当于减去了一种全部都在外面的情况。

那么双指针就可以做到 $O(n)$，但是我写的 $O(n\log n)$ 的二分。

清华集训 2024 绝顶之战

比较牛的一个题目。

考虑如果在某一个位置放置了一个物品，那么剩余的空间就会变成 $2$ 个没有关系的单独区间。

注意到 $n\le 14$，那么我们显然可以枚举一个子集 $S$，然后判断是否有一种方案可以把 $S$ 中的元素恰好放进去。

有一个性质，如果 $S$ 确定了，那么在 $[\sum\limits_{i\in S} a_i,+\infty)$ 是具有单调性的，即如果 $x$ 可以做到那么这个区间内比 $x$ 小的是都可以做到的。

上面性质的证明是容易的，我们只需要缩小之间的间距就可以了。

考虑设 $f_{i,S,T}$ 表示考虑了 $[i,n]$ 区间内的数，$T$ 里面的数不被选择，现在这一段内选择了 $S$ 的最长距离。

于是我们只需要判断是否有 $f_{1,S,[n]/S}\ge m$ 且 $\sum\limits_{i\in S} a_i\le m$ 就可以了。

考虑怎么转移，我们分情况讨论：

如果 $i\in S$，那么有转移：

$f_{i,S,T}\gets a_i+\max\limits_{S'\subseteq S} \{f_{S',T}+f_{S/S',T}\}$

如果 $i\in T$，那么有转移：

$f_{i,S,T}\gets \min(a_{i}-\varepsilon,f_{S,T/i})$

这里之所以取 $\min$ 是因为我们是从后向前转移的，如果这个位置 $i$ 可以放进去，那么就 $i$ 就肯定会放进去。

于是做完了，考虑分析时间复杂度。

因为 $S\cap T=\varnothing$，所以说一个物品在状态中会有 $3$ 中情况，分别是属于 $S$、属于 $T$ 还有都不属于，于是状态的数量就是 $O(3^n)$ 的。

然而枚举了 $S'$ 于是就相当于添加了一种状态，所以最后的复杂度就是 $O(4^n)$，可以通过。

PA 2019 Desant

一种比较神奇的状压，变进制状态存储，以前从来没有见过。

考虑最暴力的状态，我们设 $f_{i,S}$ 表示考虑了前 $i$ 个位置，选择情况为 $S$。

显然这种情况的状态数为 $O(n\times 2^n)$ 非常没有前途，考虑优化储存的信息。

对于第 $i$ 位置的数 $a_i$，在转移的时候其实并不知道前面的具体选择情况，我们只需要知道选择的数中比 $a_i$ 大的数量就可以了。

那么，我们设 $a[i+1,n]$ 排序之后得到 $x[1,n-i]$，于是我们只需要维护 $(x_{i},x_{i+1})$ 的值就可以了。

那么假设 $a_i$ 对应到 $x$ 中是 $x_j$，则我们只需要知道 $[x_j,n]$ 这个区间就行了。

于是在状压之后，转移直接枚举选与不选就行了，考虑具体怎么状压。

显然，因为 $a$ 是一个排列，那么我们需要状压的可以写成下面的形式：

第 $i$ 位需要储存的内容为 $[0,a_i]$ 的一个数，一共 $k$ 位，则令 $p_i=\prod\limits_{i=1}^ j(a_j+1)$。

那么，如果我们要储存的为 $b$，则：

$S=\sum\limits_{i=1}^ k p_i\times b_i$

考虑分析时间复杂度，不会，是 $O(n^2\times 3^{n/3})$。

ABC310Ex Negative Cost

类似于一个极大容量完全背包，考虑先消除魔力值最答案的影响，最后在单独跑超大容量背包。

我们对所有的 $C$ 取一个相反数，这样获得贡献就是 $+C_i$ 而不是 $-C_i$ 了。

很难发现所有的答案序列都可以划分成若干个所有前缀和不小于 $0$ 且所有前缀和小于 $2L-1$ 的序列，其中 $L$ 为 $C$ 可以取到的最大值。

考虑证明。

我们把这个序列按照降序进行排序，如果大小超过了 $2L-1$ 我们就从后面调遣一个负数到前面，直到前面的和 $<L$。

显然因为 $C\in [-L,+L]$，所以一定可以满足要求。

如果不存在负数了，那么我们就把还没有匹配的数都单独成一个串。

容易理解不可能出现正数不够用的情况，因为每一次剩余的和减少的量都介于 $[0,L)$ 于是固然存在一个时刻后面的处于满足要求的情况，除非本身和就小于 $0$ 但是这是不合法的。

又有另外一个性质，所有的答案序列在满足第 $1$ 个性质之后，其实还可以继续划分让每一个长度都不大于 $2L$。

记前缀和为 $s$，那么如果我们找到了两个位置 $p,q$ 满足 $s_p,s_q$，那么我们就可以把 $(p,q]$ 单独拿出来构成一个串。

如果长度大于 $2L$ 而且所有的前缀和都属于 $[-L,L]$ 之间，根绝鸽巢原理，必然存在上面的情况，于是就得证了。

那么，我们现在就得到答案一定是满足所有前缀和不小于 $0$ 且所有前缀和小于 $2L-1$ 长度不大于 $2L$ 的若干个序列拼接而成的，我们定义这样的序列为 ZDRJ 序列。

因为 ZDRJ 序列都是满足 $C\ge 0$ 的，所以通过在 ZDRJ 序列中 DP 我们就避免了来自 $C$ 的影响。

容易理解 ZDRJ 序列是很多，但是显然有些是不优秀的。

对于长度一样的 ZDRJ 序列，显然我们只需要满足伤害最高的序列就行了，那么现在我们需要考虑的就只有 $2L$ 个 ZDRJ 序列了。

考虑怎么求解最优的 ZDRJ 序列，我们设 $f_{i,j}$ 表示选择了 $i$ 个数，现在魔力值为 $j$ 的最大伤害。

那么有转移：

$f_{i,j}=\max\limits_{k=1}^{n} f_{i-1,j-c_k}+d_k$

把 ZDRJ 序列缩到一起，得到一些新的操作，其伤害和记为 $D_i$，操作次数记为 $Ct_i$。

那么我们按照 $\dfrac{D_i}{Ct_i}$ 排序，得到一个最有的 ZDRJ 序列，那么有性质：

不是最优的 ZDRJ 序列的使用次数一定不会超过 $2L$ 次。

考虑证明，容易理解的是如果某个空间可以刚好使用最优的 ZDRJ 排列的话，那么一定是最优的。

类似于前面的证明，因为最优 ZDRJ 序列的长度不会超过 $2L$。

所以如果我们把所有非性价比最优的 ZDRJ 序列拿出单独考虑，那么其前缀和一定存在 $2$ 个在模最优 ZDRJ 序列长度下同余的情况，也就是一定是存在一个区间操作数刚好是最优 ZDRJ 序列的倍数。

那么直接使用最优 ZDRJ 序列肯定不会更裂。

于是我们可以直接对不是最优的 ZDRJ 序列进行 DP，设 $g_{i}$ 表示操作次数为 $i$ 的情况下不适用最优 ZDRJ 序列的最大伤害，$f'_i=\max\limits_{j=0}^{2L} f_{i,j}$，那么有转移：

$g_i=\max\limits_{j=0}^{\min(2L,i)} g_{i-j}+f'_j$

最后用最优 ZDRJ 序列处理就可以了，总共的时间复杂度为 $O(L^3)$。

USACO22DEC Bribing Friends G

牛逼题，口爆自己都想不出来。

前 $75$ 直接暴力背包，太毒瘤了，完全不会优化，考虑转化一个思路。

按照冰淇淋从大到小排序，那么一定存在一个分界点 $p$ 满足 $p$ 前面的人全部由牟尼贿赂，而 $p$ 之后的全部由冰淇淋贿赂，而 $p$ 则二者都使用。

那么考虑利用这个性质。

设 $f_{i,j}$ 表示前 $i$ 个人用了 $j$ 个牟尼的最大好感和，而 $g_{i,j}$ 表示后 $n-i+1$ 个朋友用了 $j$ 个冰淇淋的最大好感和。

容易发现二者都是简单的 $01$ 背包，再把二者合并即可。

POI 2015 MYJ

考虑设 $f_{i,j,k}$ 表示考虑了区间 $[i,j]$ 最小值为 $k$ 的情况下的最大值。

注意到数的大小关系并不重要，那么我们将这些数离散化。

显然我们需要枚举两个区间 $[i,p)$ 和 $(p,j]$ 然后令 $p$ 取到 $k$，这样我们只需要把两侧的贡献和经过 $p$ 的贡献计算上去就好了。

一个经过 $p$ 的车子不一定最小值就在 $p$ 取，于是为了解决这个问题比较不容易想到的是我们可以只处理被 $[i,j]$ 包含且经过 $p$ 的车子。

于是我们就得到了：

$f_{i,j,k}=\max\{f_{i,p-1,y}+f_{p+1,j,z}+v(k)\times ct(p)\}$

其中 $v(k)$ 表示 $k$ 实际代表的值，而 $ct(p)$ 表示被 $[i,j]$ 包含不会放弃且经过 $p$ 的车子数量。

需要注意的是这里的 $y,z\in[k,+\infty)$，需要注意的是这里是可以取到 $k$ 的。

随便开一个数组做一个后缀最大值优化就行了，时间复杂度为 $O(n^3m)$。

事实上在转移中我们只需要用到前缀最大值就行了，于是我们可以直接将 $f$ 记录转移的位置，便于我们在分治对答案进行构造。

CSP-S2019 Emiya 家今天的饭

考虑容斥，答案为所有方案减去有一个超过 $\lfloor\dfrac{n}{2}\rfloor$ 的方案数。

做完了，$O(n^3m)$。

CF1093F Vasya and Array

设 $f_{i,j}$ 表示考虑了前 $i$ 个，结尾是 $j$ 的方案数。

枚举前面一个是哪个，一段一段放，前缀和优化，做完了。

有点难写，时间复杂度为 $O(nk)$。